By Counting Products Of The Form Xaxb Show That There Are Exactly

A by counting products of the form xaxb show that there are exactly p2p2 monic polynomials of degree 2 that are not irreducible in zp x. A by counting products of the form xaxb show that there are exactly p2p2 monic polynomials of degree 2 that are not irreducible in z p.

by counting products of the form xaxb show that there are exactly informații importante sunt însoțite de fotografii și imagini HD provenite de pe toate site-urile web din lume. Pe această pagină avem și diverse imagini atractive în PNG, JPEG, JPG, BMP, GIF, WebP, TIFF, PSD, EPS, PCX, CDR, AI, logo, pictogramă, vector, alb-negru, transparent etc.

Vă mulțumim pentru vizită, nu uitați să marcați marcajele by counting products of the form xaxb show that there are exactly folosind Ctrl + D (PC) sau Comandă + D (macros). Dacă utilizați un telefon mobil, puteți utiliza și meniul paginii de salvare printr-un browser. Orice sistem de operare folosit fie Windows, Mac, iOS sau Android poate descărca imagini folosind butonul de descărcare.

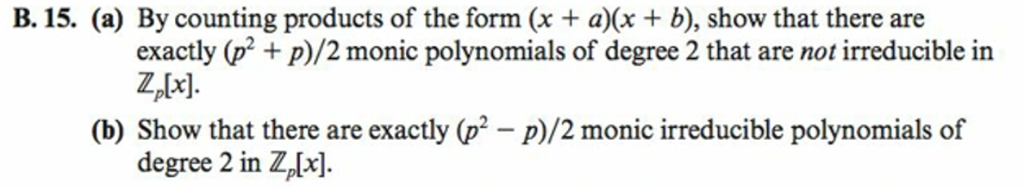Solved B 15 A By Counting Products Of The Form X A

C use a and b to show that there are exactly p 2 p 2 irreducible monic polynomials of degree 2 in z p x.

By counting products of the form xaxb show that there are exactly. So let us count the reducible monic polynomials by counting all possible pairs of roots. By counting products of the form x ax b show that thereare exactly p2 p2 monic polynomials of degree 2that are not irreducible in px. If fx gxh.

Show that there are exactly p2 p2 monic irreducible polynomials of degree 2 over z p. By counting products of the form x ax b show that there are exactly p 2 p 2 monic polynomials of degree 2 that are reducible in z p x. Since zpx is a unique factorization domain then for any pair m n of elements of zpx there is exactly one monic polynomial of degree 2 with m and n as roots namely the polynomial x mx n.

A reducible quadratic mod pcan arise in the form x a2 or x ax b. Since jz pj p there are p2 monic polynomials of degree 2 over z p. There are pof the first type and p 2 of the second type.

Math 430 algebra ii homework 2 solution based on that of liam bench 172. There are in general n 1 coefficients in front in a degree n. A monic polynomial of degree 2 over z p is determined by the two non leading coe cients.

P that there are p 1 2 values of c 2z p for which fx x2 bx cis irreducible mod p. Stack exchange network consists of 175 qa communities including stack overflow the largest most trusted online community for developers to learn share their knowledge and build their careers. A monic polynomial of degree 2 which is reducible must be of the form x ax b for ab2z p.

Every a i has p choices in z p. We must have pp 12 p2 p 2 monic irreducible quadratics in z px. So there are exactly pn elements in z pxhfxi.

An alternative and simpler proof is as follows. Count the number of monic polynomials first and then use a. Remark my hint meant to push you to show that every non zero elements in the quotient ring has.

So there are. B show that there are exactly p2 p2 monic irreducible polynomials of degree 2 in z px. X a n 1xn 1 a 0 has degree as most n 1.

Https Slidex Tips Download Problem Based Mathematics I

Composite Number Wikipedia

Sums Of Consecutive Integers Video Khan Academy

Https Slidex Tips Download Problem Based Mathematics I

Combinatorial Proofs

3 Number What Is There To Know Adding It Up Helping Children

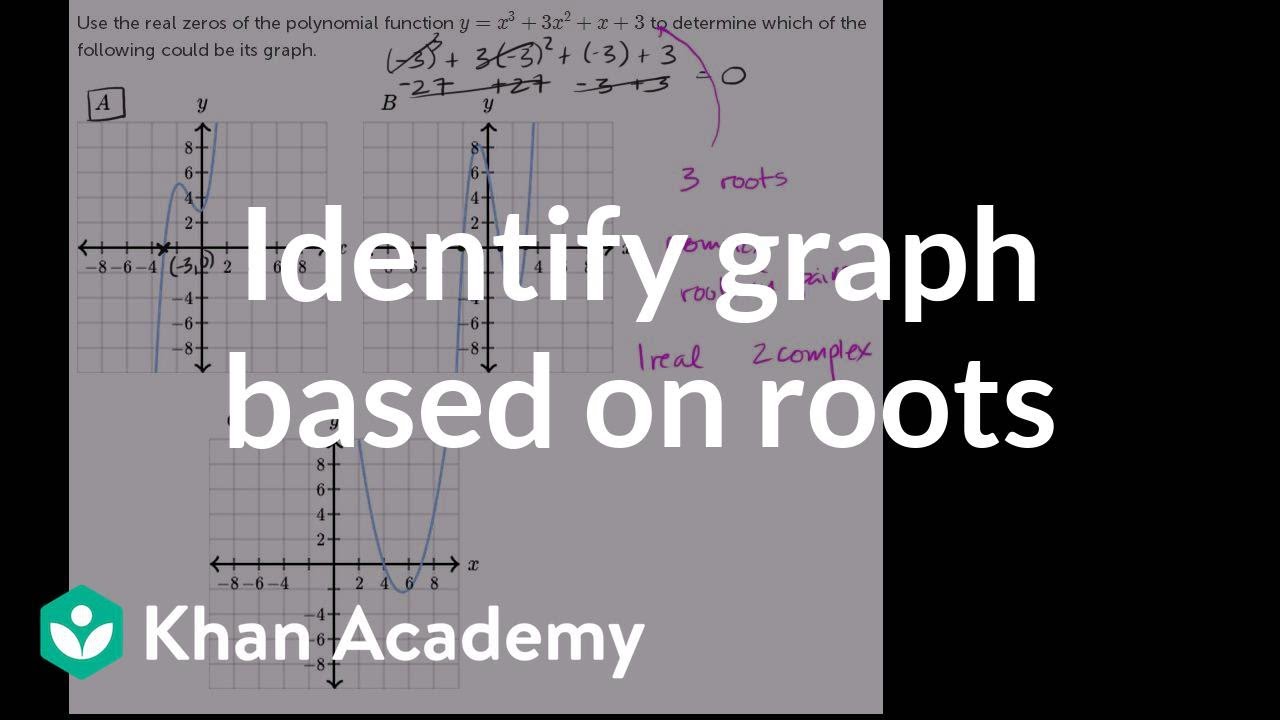Zeros Of Polynomials Their Graphs Video Khan Academy

Zeroes Of Polynomial Functions Boundless Algebra

Discrete Random Variables

Pythagorean Triangles And Triples

Gross National Product Definition Formula Examples

You have just read the article entitled By Counting Products Of The Form Xaxb Show That There Are Exactly. You can also bookmark this page with the URL : https://simptome-romania.blogspot.com/2015/12/by-counting-products-of-form-xaxb-show.html

Share Awesome